Шпаргалка: Шпора по электротехнике

Шпаргалка по электротехнике.

Дата добавления на сайт: 15 апреля 2025
Электр-кие цепи постоянного тока: элементы цепей, схемы замещения, режимы работы, анализ цепей с помощью законов Ома и Кирхгофа.
Эл-кая цепь состоит из источников и приемников эл-кой энергии,хар-мых эдс (электродвижущие силы) Е, током I, напряжением U и сопротивлением постоянному току R. Для включения и отключения электротехнических устройств применяют коммутационную аппаратуру (выключатели, рубильники, тумблеры).
Основными хар-ками элементов эл. цепей явл. зависимости их напряжения от тока. Такие зависимости наз. вольт-амперными хар-ками (в.а.х.). Элементы эл. цепи делятся на активные и пассивные. Приемники эл. энергии могут быть пассивные и активные. Пассивными наз. приемники, в кот. не возникает эдс.
Пассивный приемник, у кот. сопротивление принимается неизменным, наз. пассивным.
Закон Ома: U=RI.
1 закон Кирхгофа: алгебраическая сумма токов ветвей , сходящихся в узле, равна нулю: ∑I=0.
2 закон Кирхгофа: алгебр-кая сумма напряжений всех участков замкнутого контура равна нулю: ∑U=0, ∑RI=∑E (эдс).

Расчет сложных цепей постоянного тока с помощью законов Кирхгофа.
1 закон Кирхгофа: алгебраическая сумма токов ветвей , сходящихся в узле, равна нулю: ∑I=0. При этом токи , направленные от узла, следует брать со знаком плюс, а токи, направленные к узлу,- со знаком минус.
2 закон Кирхгофа: алгебр-кая сумма напряжений всех участков замкнутого контура равна нулю: ∑U=0, ∑RI=∑E (эдс).При этом слагаемые берут со знаком плюс в случае, когда направление обхода контура совпадает с направлением соотв-но напряжения, тока или эдс, в противном случае слагаемые берут со знаком минус.
Для определения токов ветвей цепи рекомендуется следующий порядок составления уравнений по законам Кирхгофа: определить число ветвей, узлов и независимых контуров, устанавливают число независимых уравнений по 1-му закону Кирхгофа, остальные ур-ния составляют по второму закону.
Правильность расчетов может быть проверена с помощью ур-ния баланса мощностей источников эл. энергии: ∑EI=∑RI2. В кот. правая часть хар-ет мощность пассивных приемников, а левая- мощность активных приемников.

Расчет сложных цепей постоянного тока методом контурных токов.
Суть метода заключается в следующем. Выбираются, независимые контуры (не перекрывающие друг друга) и направления контурных токов Iк в них. Записывается и решается система k алгебраических уравнений в соответствии со вторым законом Кирхгофа для каждого контура (k- число контуров):

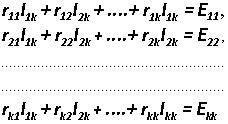
где rnk-сумма сопротивлений ветвей, входящих в контур;
Ekk - алгебраическая сумма эдс, включенных в ветви, образующие контур n.
Определяются токи ветвей Ii как алгебраические суммы (разности) соответствующих контурных токов:
.

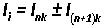Расчет сложных цепей постоянного тока методом наложения.
Ток в любой ветви может быть рассчитан как алгебраическая сумма токов, вызываемых в ней от ЭДС каждого источника напряжения в отдельности. При расчете токов, вызванных каким-либо одним источником ЭДС, другие источники ЭДС замыкаются накоротко.

Расчет сложных цепей постоянного тока методом эквивалентного генератора
Для определения тока I в произвольной ветви ав с сопротивлением r, нужно разомкнуть эту ветвь и часть цепи, подключенную к этой ветви заменить эквивалентным генератором с эдс Еr и внутренним сопротивлением rr.Расчет Еr ведется любым известным способом. Расчет rr ведут полагая, что оно равно входному сопротивлению цепи с закороченными источниками эдс относительно ав. Определяют ток в искомой ветви:

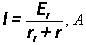
Нелинейные цепи постоянного тока. Графический метод расчета.
Нелинейными называются цепи, в состав которых входит хотя бы один нелинейный элемент.
Нелинейными называются элементы, параметры которых зависят от величины и (или) направления связанных с этими элементами переменных (напряжения, тока, магнитного потока, заряда, температуры, светового потока и др.). Нелинейные элементы описываются нелинейными характеристиками, которые не имеют строгого аналитического выражения, определяются экспериментально и задаются таблично или графиками.
а) Цепи с последовательным соединением резистивных элементов.

При последовательном соединении нелинейных резисторов в качестве общего аргумента принимается ток, протекающий через последовательно соединенные элементы. Расчет проводится в следующей последовательности. По заданным ВАХ отдельных резисторов в системе декартовых координат строится результирующая зависимость. Затем на оси напряжений откладывается точка, соответствующая в выбранном масштабе заданной величине напряжения на входе цепи, из которой восстанавливается перпендикуляр до пересечения с зависимостью. Из точки пересечения перпендикуляра с кривой опускается ортогональ на ось токов – полученная точка соответствует искомому току в цепи, по найденному значению которого с использованием зависимостей определяются напряжения на отдельных резистивных элементах.

Применение указанной методики иллюстрируют графические построения на рис. 2,б, соответствующие цепи на рис. 2,а.


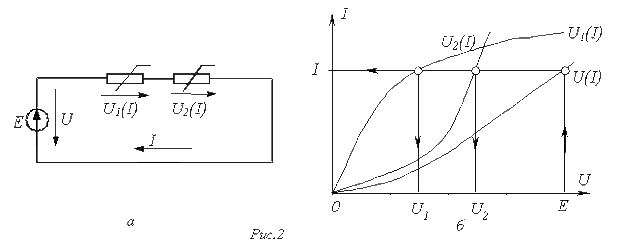
Графическое решение для последовательной нелинейной цепи с двумя резистивными элементами может быть проведено и другим методом – методом пересечений. В этом случае один из нелинейных резисторов, например, с ВАХ на рис.2,а, считается внутренним сопротивлением источника с ЭДС Е, а другой – нагрузкой. Тогда на основании соотношения точка а (см. рис. 3) пересечения кривых и определяет режим работы цепи. Кривая строится путем вычитания абсцисс ВАХ из ЭДС Е для различных значений тока.

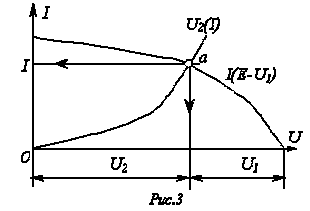
Использование данного метода наиболее рационально при последовательном соединении линейного и нелинейного резисторов. В этом случае линейный резистор принимается за внутреннее сопротивление источника, и линейная ВАХ последнего строится по двум точкам.
б) Цепи с параллельным соединением резистивных элементов.
При параллельном соединении нелинейных резисторов в качестве общего аргумента принимается напряжение, приложенное к параллельно соединенным элементам. Расчет проводится в следующей последовательности. По заданным ВАХ отдельных резисторов в системе декартовых координат строится результирующая зависимость . Затем на оси токов откладывается точка, соответствующая в выбранном масштабе заданной величине тока источника на входе цепи (при наличии на входе цепи источника напряжения задача решается сразу путем восстановления перпендикуляра из точки, соответствующей заданному напряжению источника, до пересечения с ВАХ ), из которой восстанавливается перпендикуляр до пересечения с зависимостью . Из точки пересечения перпендикуляра с кривой опускается ортогональ на ось напряжений – полученная точка соответствует напряжению на нелинейных резисторах, по найденному значению которого с использованием зависимостей определяются токи в ветвях с отдельными резистивными элементами.
Использование данной методики иллюстрируют графические построения на рис. 4,б, соответствующие цепи на рис. 4,а.

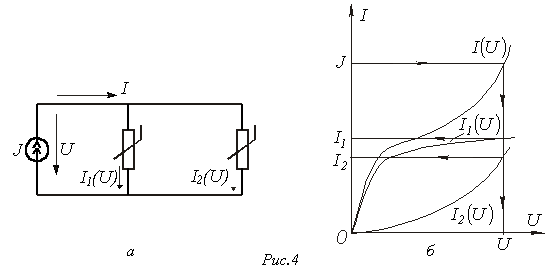
в) Цепи с последовательно-параллельным (смешанным) соединением резистивных элементов.
1. Расчет таких цепей производится в следующей последовательности:
Исходная схема сводится к цепи с последовательным соединением резисторов, для чего строится результирующая ВАХ параллельно соединенных элементов, как это показано в пункте б).
2. Проводится расчет полученной схемы с последовательным соединением резистивных элементов (см. пункт а), на основании которого затем определяются токи в исходных параллельных ветвях.

Однофазные цепи синусоидального тока: элементы цепей, схемы замещения. Активное, реактивное и полное сопротивление. Треугольник сопротивлений. Законы Ома и Кирхгофа.
Переменными наз. эдс, токи и напряжения, изменяющиеся с течением времени. Значение переменного тока в рассматриваемый момент времени называют мгновенным значением и обозначают строчной буквой i.
Мгновенный ток называется периодическим, если значения его повторяются через одинаковые промежутки времени:
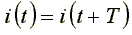
Наименьший промежуток времени, через который значения переменного тока повторяются, называется периодом.
Период T измеряется в секундах. Периодические токи, изменяющиеся по синусоидальному закону, называются синусоидальными.
Мгновенное значение синусоидального тока определяется по формуле

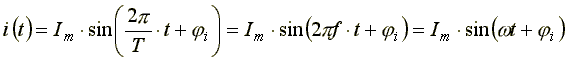
где Im - максимальное, или амплитудное, значение тока.
Аргумент синусоидальной функции 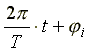называют фазой; величину φ, равную фазе в момент времени t = 0, называют начальной фазой. Фаза измеряется в радианах или градусах. Величину, обратную периоду, называют частотой. Частота f измеряется в герцах.
Величину 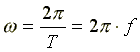называют круговой, или угловой, частотой. Угловая частота измеряется в рад/c.
Действующим значением переменного тока называется среднеквадратичное значение тока за период. Действующее значение тока (для синусоиды ):

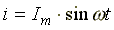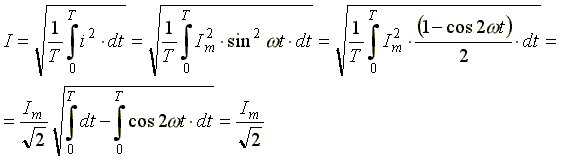
Аналогично определяются действующие значения ЭДС и напряжений
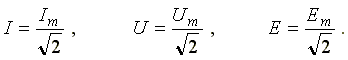
Закон Ома для мгновенных значений:
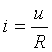
Законы Кирхгофа для мгновенных значений: , .
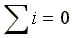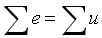Активное сопротивление(R)- сопротивление резисторного элемента R в цепи переменного тока.
Реактивное сопротивление- коэф. при мнимой части комплексного сопротивления (Х): Х= ХL-ХС.
ХL-индуктивное сопротивление XL=Lѡ, ХC- емкостное сопротивление XC=1/Cѡ.
Полное сопротивлениеZ-модуль комплексного сопр-ия, равен отношению амплитуды напряжения к амплитуде тока, а аргумент комплексного сопр-ия- разности начальных фаз напряжения и тока: Z= UmIm, φ=φu-φi.
Рассмотрим соотношение,связывающее полное сопр-иеZ с активным R и реактивным X. Заштрихованный треугольник наз. треугольником сопротивлений. Из него очевидны соотношения:
Z=R2+X2, tanφ=XR, cosφ=RZ, sinφ=XZ, R=Zcosφ, X=Zsinφ.
Последовательная цепь R, L, C (векторная диаграмма, фазовые соотношения между током и напряжением, законы Ома и Кирхгофа).
Уравнение напряжений для цепи (рис. 1а) имеет вид: Ū = Ūr + Ūl+ Ūc

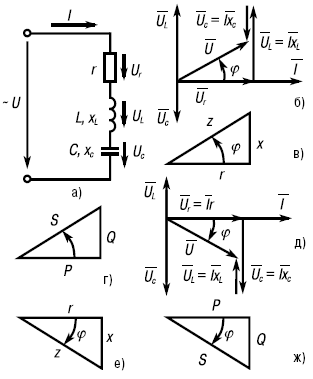
Рис. 1. Электрическая цепь, содержащая последовательно включенные r, L и С (а), ее векторная диаграмма (б), треугольники сопротивлений и мощностей (в и г) цепи при xL > xC, векторная диаграмма (д), треугольники сопротивлений и мощностей (е и ж) цепи при xC > xL.

Векторные диаграммы для цепи (рис. 1а) изображены на рисунках 1б и 1в. Вектор напряжения на активном сопротивлении совпадает с вектором тока, вектор напряжения на индуктивности Ūl опережает вектор тока на 90°, вектор напряжения на емкости Ūc отстает от вектора тока на 90°. Следовательно, между векторами напряжения на индуктивности и емкости образуется угол в 180°.

Если xL > xC, то и UL > Ūc и векторная диаграмма будет такой (см. рис. 1б), а треугольник сопротивлений – на рисунке 17в, где x = xL – xC. Если xC > xL, то UC > UL и векторная диаграмма будет иметь вид, изображенный на рисунке 17е, где x = xC – xL.
Значение напряжения, приложенного к цепи:
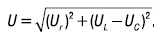
Выразив напряжение через ток и сопротивления, получим

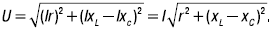
Последнее выражение представляет собой закон Ома для последовательной цепи r, L, C:


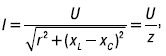
где z – полное сопротивление цепи;
x – реактивное сопротивление цепи.
На основании проведенного анализа цепи, состоящей из последовательно соединенных r, L, C, можно сделать следующие выводы.
Если xL > xC, то напряжение сети опережает по фазе ток на угол φ: υ = Um sin (ωt + φ).
Цепь имеет активно(индуктивный характер.
Если xC > xL, то напряжение сети отстает по фазе от тока на угол φ: υ = Um sin (ωt + φ).
Цепь имеет активно(емкостный характер.

Параллельное соединение приемников синусоидального тока (законы Ома и Кирхгофа, векторная диаграмма).
Рис.1
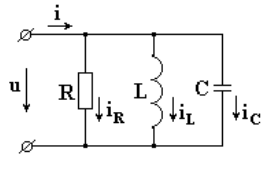
Если к выводам электрической цепи, состоящей из параллельно соединенных R, L, C (рис. 1), приложено синусоидальное напряжение то по I закону Кирхгофа синусоидальный ток в неразветвленной части равен алгебраической сумме синусоидальных токов в параллельных ветвях
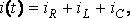
где 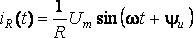– совпадает по фазе с напряжением u(t);

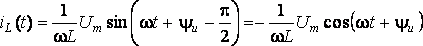– отстает по фазе от напряжения u(t) на ;
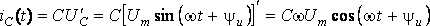– опережает по фазе напряжение u(t) на .
Просуммируем:



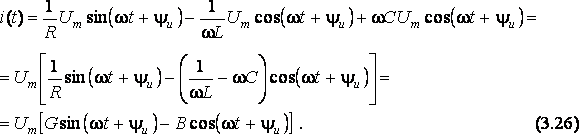
Выражение (3.26) является тригонометрической формой записи I закона Кирхгофа для мгновенных значений.

Активная проводимость цепи 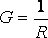, всегда положительна.

Реактивная проводимость цепи 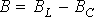, в зависимости от знака может иметь индуктивный (В > 0) или емкостный (B 0; при этом ток опережает по фазе напряжение.

– при емкостном характере цепи, т.е. при B U1).

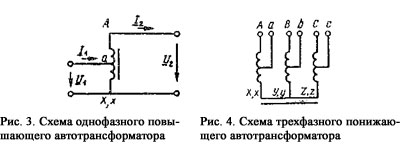
Широкое применение находят также и трехфазные автотрансформаторы. Схема такого автотрансформатора показана на рис. 4. Обмотки трехфазного автотрансформатора соединяют чаще всего в звезду.
Автотрансформаторы мощностью до 1 кВ·А широко применяются в автоматике и бытовой технике. Более мощные автотрансформаторы используются для понижения напряжения при пуске мощных двигателей переменного тока. Силовые автотрансформаторы большой мощности находят применение для соединения между собой электрических сетей повышенных напряжений с близкими уровнями этих напряжений. Мощность таких автотрансформаторов достигает нескольких сотен мегавольт-ампер.
Силовые автотрансформаторы, как правило, имеют дополнительную обмотку НН (6-35 кВ), соединенную в треугольник. Эта обмотка не имеет электрической связи с основными обмотками автотрансформатора и служит для компенсации третьих гармонических составляющих потоков или потоков нулевой последовательности. Иногда ее используют для электроснабжения местных потребителей.
Все обмотки каждой фазы автотрансформатора (включая и дополнительную обмотку) располагаются на одном стержне в виде концентрических катушек одной высоты, что способствует уменьшению их индуктивных сопротивлений рассеяния. Ближе к стержню располагается обмотка НН.
Эти автотрансформаторы предназначаются для работы в трехфазной группе.

Трехфазные асинхронные двигатели (АД). Устройство и принцип работы, уравнения электрического и магнитного состояния. Магнитное поле машин.
Неподвижная часть машины называется статор, подвижная – ротор. Сердечник статора набирается из листовой электротехнической стали и запрессовывается в станину. На рис. 2.1 показан сердечник статора в сборе. Станина (1) выполняется литой, из немагнитного материала. Чаще всего станину выполняют из чугуна или алюминия. На внутренней поверхности листов (2), из которых выполняется сердечник статора, имеются пазы, в которые закладывается трёхфазная обмотка (3). Обмотка статора выполняется в основном из изолированного медного провода круглого или прямоугольного сечения, реже – из алюминия.
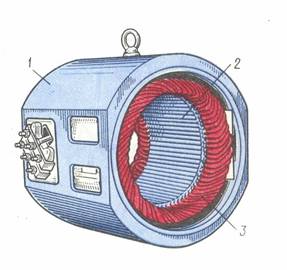рис 2.1
Обмотка статора состоит из трёх отдельных частей, называемых фазами. Начала фаз обозначаются буквами с1, с2, с3, концы – с4, с5, с6.
Начала и концы фаз выведены на клеммник (рис. 2.2 а), закреплённый на станине. Обмотка статора может быть соединена по схеме звезда (рис. 2.2 б) или треугольник (рис. 2.2 в). Выбор схемы соединения обмотки статора зависит от линейного напряжения сети и паспортных данных двигателя. В паспорте трёхфазного двигателя задаются линейные напряжения сети и схема соединения обмотки статора. Например, 660/380, Y/∆. Данный двигатель можно включать в сеть с Uл = 660В по схеме звезда или в сеть с Uл =380В – по схеме треугольник.
Основное назначение обмотки статора – создание в машине вращающего магнитного поля.
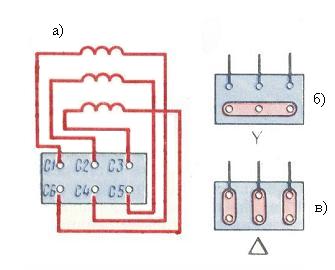рис 2.2

а) ЭДС статора.
Магнитное поле, создаваемое обмоткой статора, вращается относительно неподвижного статора с частотой n0 = (60 f) / p и будет наводить в обмотке статора ЭДС. Действующее значение ЭДС, наводимой этим полем в одной фазе обмотки статора определяется выражением:
E1 = 4,44 w1 k1 f Ф,
где: k1=0.92÷0.98 – обмоточный коэффициент;
f1=f – частота сети;
w1 – число витков одной фазы обмотки статора;
Ф – результирующее магнитное поле в машине.
б) Уравнение электрического равновесия фазы обмотки статора.
Это уравнение составлено по аналогии с катушкой с сердечником, работающей на переменном токе.

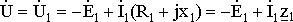
Здесь Ú и Ú1 – напряжение сети и напряжение, подведённое к обмотке статора.
R1 – активное сопротивление обмотки статора, связанное с потерями на нагрев обмотки.
x1 – индуктивное сопротивление обмотки статора, связанное с потоком рассеяния.
z1 – полное сопротивление обмотки статора.
İ1 – ток в обмотке статора.
При анализе работы асинхронных машин часто принимают I1 z1 = 0. Тогда можно записать:
U1 ≈ E1 = 4,44 w1 k1 f Ф.
Из этого выражения следует, что магнитный поток Ф в асинхронной машине не зависит от её режима работы, а при заданной частоте сети ƒ зависит только от действующего значения приложенного напряжения U1. Аналогичное соотношение имеет место и в другой машине переменного тока – в трансформаторе.
Направление вращения магнитного поля зависит от порядка чередования фаз. Величина результирующей магнитной индукции 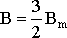. Частота вращения магнитного поля n0 зависит от частоты сети f и числа пар полюсов магнитного поля р. n0 = (60 f) / p, [об/мин]. Частота вращения магнитного поля не зависит от режима работы асинхронной машины и её нагрузки. При анализе работы асинхронной машины часто используют понятие о скорости вращения магнитного поля ω0, которая определяется соотношением:ω0 = (2 π f) / p = π n0 / 30, [рад/сек].
а) Частота ЭДС и тока ротора.
При неподвижном роторе частота ЭДС f2 равна частоте сети f. f2 = f = (n0 p) / 60.
При вращающемся роторе частота ЭДС ротора зависит от частоты вращения магнитного поля относительно вращающегося ротора, которая определяется соотношением:
n\' = n0 - n.
Тогда частота ЭДС вращающегося ротора:
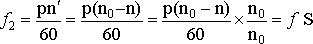
Частота ЭДС ротора изменяется пропорционально скольжению и в режиме двигателя имеет наибольшее значение в момент пуска в ход.
Пусть при f = 50 Гц, номинальное скольжение Sн = 2 %. Тогда при номинальной частоте вращения ротора f2 = f × Sн = 1 Гц.
Таким образом, в обмотке ротора асинхронной машины частота наводимой ЭДС зависит от частоты вращения ротора.

Электромагнитный момент АД. Механические хар-ки.
Электромагнитный момент возникает при наличии магнитного поля, создаваемого обмоткой статора, и тока в обмотке ротора. Можно показать, что электромагнитный момент определяется соотношением: М=СФI2cosψ2.
Здесь 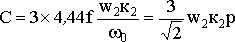– конструктивный коэффициент;
ω0 = 2 π f / p – скорость вращения магнитного поля;
ψ2 – сдвиг по фазе между ЭДС и током ротора;
I2 cos ψ2– активная составляющая тока ротора.
Таким образом, величина электромагнитного момента зависит от результирующего магнитного поля Ф и активной составляющей тока ротора.
Под механической характеристикой принято понимать зависимость частоты вращения ротора в функции от электромагнитного момента n = f(M). Эту характеристику (рис. 2.15) можно получить, используя зависимость M = f(S) и пересчитав частоту вращения ротора при разных значениях скольжения.
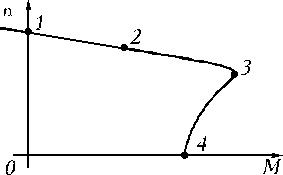рис 2.15
Так как S = (n0 - n) / n0, отсюда n = n0(1 - S). Напомним, что n0 = (60 f) / p – частота вращения магнитного поля.

Участок 1-3 соответствует устойчивой работе, участок 3-4 – неустойчивой работе. Точка 1 соответствует идеальному холостому ходу двигателя, когда n = n0. Точка 2 соответствует номинальному режиму работы двигателя, ее координаты Мн и nн. Точка 3 соответствует критическому моменту Мкр и критической частоте вращения nкр. Точка 4 соответствует пусковому моменту двигателя Мпуск. Механическую характеристику можно рассчитать и построить по паспортным данным. Точка 1:
n0 = (60 f) / p,
где: р – число пар полюсов машины;
f – частота сети.
Точка 2 с координатами nн и Мн. Номинальная частота вращения nн задается в паспорте. Номинальный момент рассчитывается по формуле:
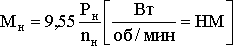
здесь: Рн – номинальная мощность (мощность на валу).
Точка 3 с координатами Мкр nкр. Критический момент рассчитывается по формуле Мкр = Мн λ. Перегрузочная способность λ задается в паспорте двигателя nкр = n0 (1 - Sкр), , Sн = (n0 - nн) / n0 – номинальное скольжение.
Точка 4 имеет координаты n=0 и М=Мпуск. Пусковой момент вычисляют по формуле
Мпуск = Мн λпуск,
где: λпуск – кратность пускового момента задается в паспорте.
Асинхронные двигатели имеют жесткую механическую характеристику, т.к. частота вращения ротора (участок 1–3) мало зависит от нагрузки на валу. Это одно из достоинств этих двигателей.

Пуск АД с короткозамкнутым и фазным ротором. Регулирование частоты вращения.
В момент пуска в ход n=0, т.е. скольжение S=1. Т.к. токи в обмотках ротора и статора зависят от скольжения и возрастают при его увеличении, пусковой ток двигателя в 5 ÷ 8 раз больше его номинального тока Iпуск = (5 ÷ 8) Iн.
Как рассматривалось ранее, из-за большой частоты ЭДС ротора асинхронные двигатели имеют ограниченный пусковой момент Мпуск = (0,8 ÷ 1,8) Мн.
Для пуска в ход двигателя необходимо, чтобы развиваемый им пусковой момент превышая момент нагрузки на валу. В зависимости от мощности источников питания и условий пуска используют разные способы пуска, которые преследуют цели: уменьшение пускового тока и увеличение пускового момента.
Различают следующие способы пуска в ход асинхронных двигателей: прямое включение в цепь, пуск при пониженном напряжении, реостатный пуск, использование двигателей с улучшенными пусковыми свойствами.
1. Прямое включение в сеть
Это самый простой и самый дешевый способ пуска. На двигатель вручную или с помощью дистанционного управления подается номинальное напряжение. Прямое включение в сеть допускается, если мощность двигателя не превышает 5% от мощности трансформатора, если от него питается и осветительная сеть.
2. Пуск при пониженном напряжении
Этот способ применяют при пуске в ход мощных двигателей, для которых недопустимо прямое включение в сеть. Для понижения подводимого к обмотке статора напряжения используют дроссели и понижающие автотрансформаторы. После пуска в ход на обмотку статора подается напряжение сети.
Основные недостатки этого способа пуска: высокая стоимость пусковой аппаратуры и невозможность пуска с нагрузкой на валу.
3. Реостатный пуск асинхронных двигателей
Этот способ применяют при тяжелых условия пуска, т.е. при большой нагрузке на валу. Для реостатного пуска используют асинхронные двигатели с фазным ротором, в цепь ротора включается пусковой реостат. Реостатный пуск служит для увеличения пускового момента. Одновременно происходит уменьшение пускового тока двигателя. По мере разгона двигателя пусковой реостат выводится и после окончания пуска обмотка ротора оказывается замкнутой накоротко.
Критическое скольжение равно:
для естественной характеристики ;
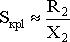для искусственной характеристик и.
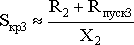Пусковой момент для искусственной характеристики можно рассчитать по формуле Клосса
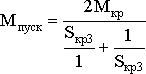
Задаваясь необходимой величиной пускового момента, можно вычислить Sкр3 и величину пускового сопротивления .
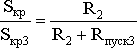4. Использование двигателей с улучшенными пусковыми свойствами
Стремление совместить достоинства асинхронных двигателей с короткозамкнутым ротором (высокая надежность) и фазным ротором (большой пусковой момент) привело к созданию этих двигателей. Они имеют короткозамкнутую обмотку ротора специальной конструкцией. Различают двигатели с обмоткой ротора в виде двойной «беличьей клетки» и с глубоким пазом.
У двигателя с двойной «беличьей клеткой» на роторе закладывается две короткозамкнутые обмотки. Обмотка 1 выполняет роль пусковой, а обмотка 2 является рабочей. Для получения повышенного пускового момента пусковая обмотка должна обладать большим активным сопротивлением, чем рабочая обмотка. Поэтому обмотка 1 выполняется из материала с повышенным удельным сопротивлением (латунь), чем обмотка 2 (медь). Сечение проводников, образующих пусковую обмотку, меньше, чем у рабочей обмотки. За счет этого повышается активное сопротивление пусковой обмотки.
Аналогичная картина наблюдается у двигателя с глубоким пазом. Глубокий стержень обмотки (1) можно представить в виде нескольких проводников, расположенных по высоте паза. За счет высокой частоты тока в обмотке ротора в момент пуска в ход происходит «вытеснение тока к поверхности проводника». За счет этого в создании пускового момента участвует только верхний слой проводников обмотки ротора. Сечение верхнего слоя значительно меньше сечения всего проводника. Поэтому при пуске в ход обмотка ротора обладает повышенным активным сопротивлением, двигатель развивает повышенный пусковой момент. По мере разгона двигателя плотность тока по сечению проводников обмотки ротора выравнивается, сопротивление обмотки ротора снижается.

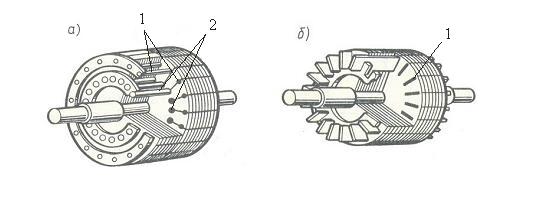
А) двойная «беличья клетка» Б) глубокий паз.
В целом эти двигатели имеют жесткие механические характеристики, повышенный пусковой момент и меньшую кратность пускового тока, чем двигатели с короткозамкнутым ротором обычной конструкцией.
При работе многих механизмов, приводящихся во вращение асинхронными двигателями, в соответствии с технологическими требованиями возникает необходимость регулировать скорость вращения этих механизмов. Способы регулирования частоты (скорости) вращения асинхронных двигателей раскрывает соотношение:
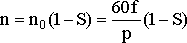
Отсюда следует, что при заданной нагрузке на валу частоту вращения ротора можно регулировать:
изменением скольжения;
изменением числа пар полюсов;
изменением частоты источника питания.

Автоматическое управление асинхронным двигателем.
Автоматизация управления короткозамкнутым асинхронным двигателем. Принципы автоматизации управления электродвигателями легче всего уяснить, начав рассмотрение с наиболее простой схемы автоматизации пуска, реверса и защиты короткозамкнутого асинхронного двигателя (рис. 17.19). Аппаратура управления содержит, реверсивный магнитный пускатель, кнопочную станцию, тепловые реле, предохранители, выключатель. Питание двигателя и цепи управления - от одной сети.
При включении выключателя «Вкл.» схема готова к работе. Нажатием кнопки, например, «Вперед», включают катушку контактора В. Срабатывая, он замыкает свои главные контакты В и присоединяет двигатель к сети. Одновременно замыкается его блок-контакт В, блокирующий кнопку «Вперед». Для остановки двигателя нажимают кнопку «Стоп». Цепь катушки контактора В разрывается, контактор отключается и отсоединяет двигатель от сети. Одновременное нажатие на кнопки «Вперед» И «Назад» исключено за счет механической связи контактов в цепях катушек В и Н.
Автоматическая защита двигателя от длительных -перегрузок осуществляется биметаллическими тепловыми реле РТ 1. и РТ2, размыкающие контакты которых включены в цепь питания обмоток контакторов. От кратковременных пусковых токов реле не успевают сработать. При перегрузке реле срабатывают, выключая контактор: двигатель отключается от сети. Возврат контактов после остывания биметаллической пластинки производится вручную, после устранения причины перегрузки. Защита от токов короткого замыкания обеспечивается плавкими предохранителями. Они не срабатывают от пусковых токов. Предусмотрена также «нулевая защита»: при исчезновении или значительном снижении напряжения сети контактор отключается и отсоединяет двигатель от сети.




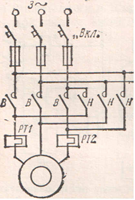
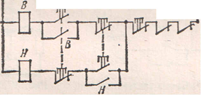
Защита асинхронного двигателя от перегрузки и обрыва фаз
Виды защиты асинхронных электродвигателей.
Для того чтобы защитить электродвигатель от повреждений при нарушении нормальных условий работы, а также своевременно отключить неисправный двигатель от сети, предотвратив или ограничив тем самым развитие аварии, предусматриваются средства защиты.
Главным и наиболее действенным средством является электрическая защита двигателей, выполняемая в соответствии с «Правилами устройства электроустановок» (ПУЭ).
В зависимости от характера возможных повреждений и ненормальных режимов работы различают несколько основных наиболее распространенных видов электрической защиты асинхронных двигателей.
Защита асинхронных электродвигателей от перегрузки
Защита от перегрузки предохраняет двигатель от недопустимого перегрева, в частности и при сравнительно небольших по величине, но продолжительных тепловых перегрузках. Защита от перегрузки должна применяться только для электродвигателей тех рабочих механизмов, у которых возможны ненормальные увеличения нагрузки при нарушениях рабочего процесса.
Аппараты защиты от перегрузки (тепловые и температурные реле, электромагнитные реле, автоматические выключатели с тепловым расцепителем или с часовым механизмом) при возникновении перегрузки отключают двигатель с определенной выдержкой времени, тем большей, чем меньше перегрузка, а в ряде случаев, при значительных перегрузках, — и мгновенно.
Защита асинхронных электродвигателей от понижения или исчезновения напряжения
Защита от понижения или исчезновения напряжения (нулевая защита) выполняется с помощью одного или нескольких электромагнитных аппаратов, действует на отключение двигателя при перерыве питания или снижении напряжения сети ниже установленного значения и предохраняет двигатель от самопроизвольного включения после ликвидации перерыва питания или восстановления нормального напряжения сети.
Специальная защита от работы на двух фазах предохраняет двигатель от перегрева, а также от «опрокидывания», т. е. остановки под током вследствие снижения момента, развиваемого двигателем, при обрыве в одной из фаз главной цепи. Защита действует на отключение двигателя.
В качестве аппаратов защиты применяются как тепловые, так и электромагнитные реле. В последнем случае защита может не иметь выдержки времени.


Устройство и принцип действия трехфазного синхронного двигателя (СД), пуск и область применения. Электромагнитный момент СД и угловые хар-ки.
Синхронная машина состоит из двух основных частей: неподвижной - статора и вращающейся - ротора, и имеет две основные обмотки. Одна обмотка подключается к источнику постоянного тока. Протекающий по этой обмотке ток создает основное магнитное поле машины. Эта обмотка располагается на полюсах и называется обмоткой возбуждения. Иногда у машин небольшой мощности обмотка возбуждения отсутствует, а магнитное поле создается постоянными магнитами. Другая обмотка является обмоткой якоря. В ней индуктируется основная ЭДС машины. Она укладывается в пазы якоря и состоит из одной, двух или трех обмоток фаз. Наибольшее распространение в синхронных машинах нашли трехфазные обмотки якоря.
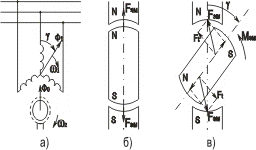рис 3.2
Обмотка статора подключается к трехфазной сети переменного тока с частотой f и обмотка создает магнитное поле ω1, вращающееся с угловой скоростью ω1=2πf/РМ (рис.3.2, а). Индуктор создает постоянный поток возбуждения Ф0. При вращении ротора с постоянной скоростью ω2=ω1 поля статора и ротора неподвижны друг относительно друга и в результате их взаимодействия создается электромагнитный момент Mэм. Если ротор отстает по углу от поля статора, то момент направлен в сторону вращения ротора (является вращающим) и с вала двигателя снимается механическая энергия.
Более наглядно процесс возникновения электромагнитного момента можно рассмотреть на статической модели (рис.3.2, б, в), в которой статор и ротор заменены неподвижными постоянными магнитами. В положении, изображенном на рис.3.2,б, угол между полями статора и ротоpa равен нулю, силы притяжения разноименных полюсов статора и ротора Fэм не имеют тангенциальной составляющей и Mэм=0. Ротор находится в положении устойчивого равновесия. Повернем ротор относительно полюсов статора на угол γ (рис. 3.2, в). У сил притяжения Fэм появляются тангенциальные составляющие Ft ,и создается момент Мэм, стремящийся вернуть ротор в исходное положение. Нетрудно заметить, что максимальное значение момента будет при γ = 90°. При γ= 180° момент Мэм снова равен нулю, но это положение неустойчивого равновесия ротора, т.к. между одноименными полюсами статора и ротора действуют силы отталкивания. Достаточно малейшего отклонения угла γ от 180° и эти силы вернут ротор в положение γ = 0 (понятия положений устойчивого и неустойчивого положений ротора соответствуют аналогичным понятиям у обычного физического маятника).
Следовательно, в первом приближении можно считать, что в синхронном двигателе с электромагнитным возбуждением электромагнитный момент изменяется по закону Мэм=Ммaxsin γ. Этот момент Мэм часто называют синхронизирующим. При числе пар полюсов рм> I вместо угла γ должен быть взят электрический угол γэ= рм γ. В соответствии с уравнением равновесия моментов в установившемся режиме Мэм= Мст= М0+Мн. Значит, чем больше момент нагрузки Мн на валу двигателя, тем на больший угол отстает ротор от поля статора. Значение момента сопротивления Мст не должно превышать Ммax, т.к. в противном случае равновесие моментов не устанавливается при любых значенияхγ в диапазоне от 0° до 360° и ротор выходит из синхронизма – начинает отставать от поля статора по угловой скорости. Поэтому Ммax называют моментом выхода из синхронизма. Практически рабочий диапазон моментов выбирается таким образом, чтобы γ не превышал 20° –30°.
Пуск синхронных двигателей.
У синхронных двигателей без пусковой обмотки среднее значение пускового момента, развиваемого двигателем, равно нулю. Объясняется это тем, что при ω2≠ω1 угол γ=(ω1-ω2)рмt, т.е. при ω2=0 изменяется во времени с частотой ω=2πf. С этой частотой изменяется и мгновенное значение электромагнитного момента, направление момента дважды изменяется за период оборота поля статора. Ротор, обладающий значительным моментом инерции, за полпериода не может успеть разогнаться до синхронной скорости: под действием пульсирующего момента он вибрирует в положении устойчивого равновесия и во вращение не приходит. Поэтому для пуска синхронных двигателей применяются специальные способы, наиболее распространенным из которых является асинхронный способ пуска (рис.3.З, а).

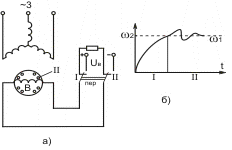
Рис. 3.3
Для реализации этого способа на роторе двигателя, как уже отмечалось, располагается короткозамкнутая пусковая обмотка П. В начальный период пуска (переключатель Пер в положении 1) обмотка возбуждения В ротора отключена от источника и замкнута на сопротивление с целью снятия перенапряжении и создания дополнительного пускового момента. Двигатель работает как обычный асинхронный двигатель, и под действием асинхронного пускового момента ротор начинает разгоняться (рис.3.3, б). При достижении угловой скорости ω2≈0.95ω1 переключатель переводится в положение II. Появляется поток возбуждения индуктора, и создается синхронный электромагнитный момент. Частота пульсаций этого момента (ω1-ω2)рм близка к собственной частоте ротора, ротор начинает раскачиваться и в процессе качаний входит в синхронизм. Наибольший момент сопротивления, при котором ротор еще втягивается в синхронизм, называется моментом входа. Реверсирование двигателя осуществляется изменением направления вращения магнитного поля.


Регулирование реактивной мощности СД. Синхронный компенсатор.

Комментарии:

Вы не можете оставлять комментарии. Пожалуйста, зарегистрируйтесь.